CSAPP:lab:cache

发表于 2023-10-19 更新于 2024-06-09 分类于 CSAPP ， lab

Cache Lab

本文章不含具体代码实现，具体实现在 Github

Introduction

为什么需要Cache

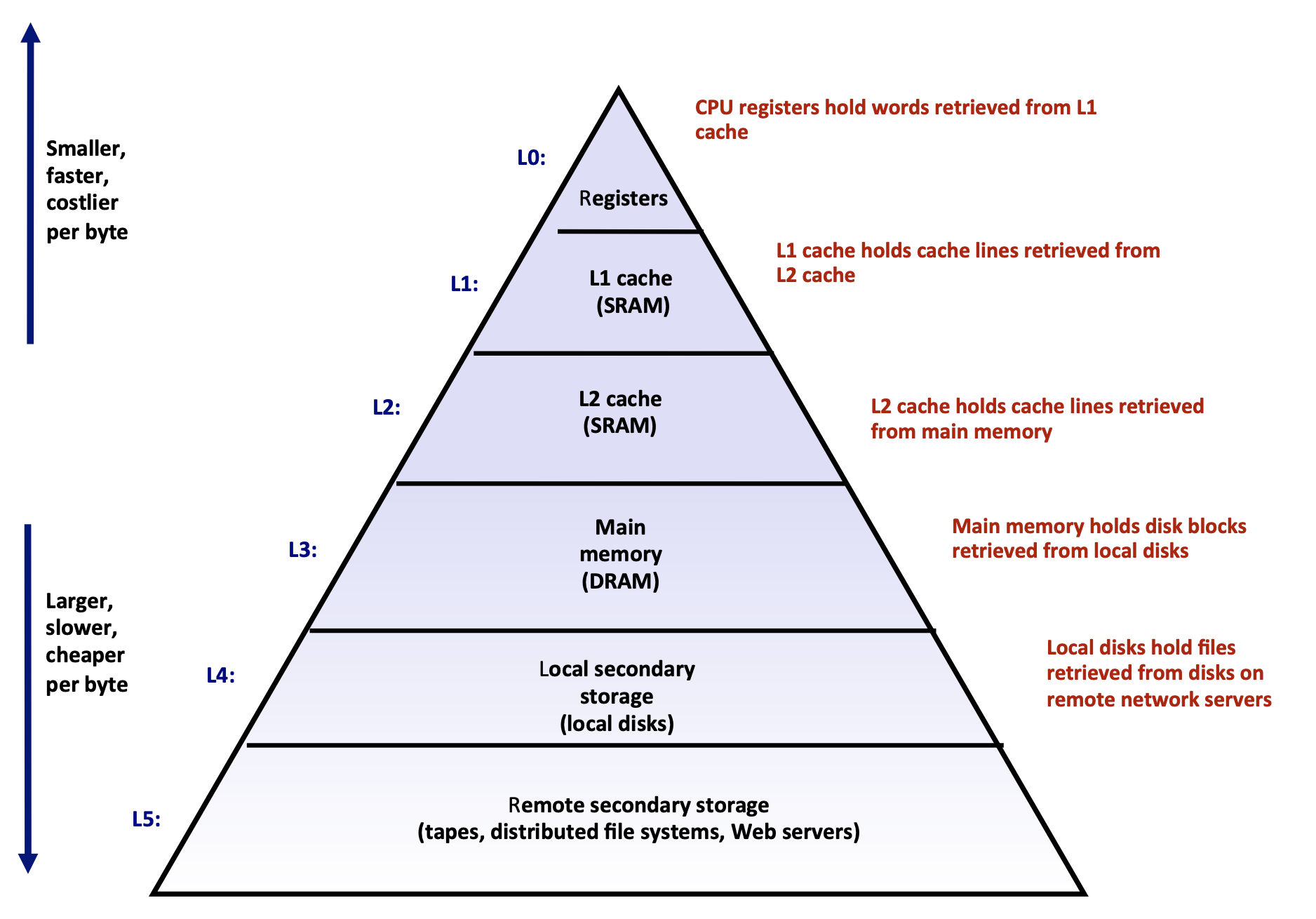
由这张经典的分层图，由下至上速度更快，价格更贵。那么在工程上考虑，如何能更好得利用这些不同处理能力的存储设备就很关键。Generally specking，每下一层都可以理解为是上一层的cache。
Cache 可以最大化利用程序的时间局部性、空间局部性。

Cache memory

Cache memories are small, fast SRAM-based memories managed automatically in hardware.
- 更小、更快、更贵的memory cache是更大、更慢、更便宜的memory的副本子集，单位为block。
Cache Organization (以64位机器为例):

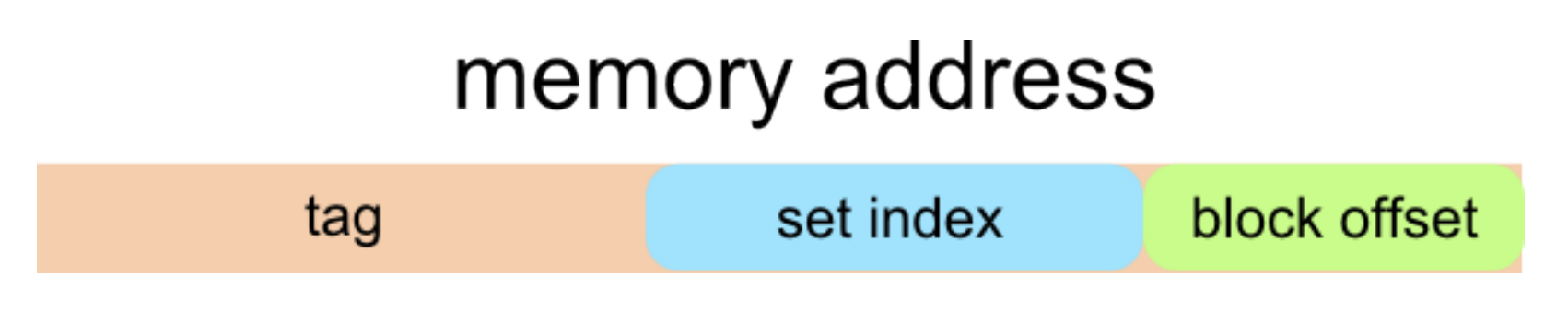
Block offset: b bits

Set index: s bits

Tag Bits: (Address Size - b - s)

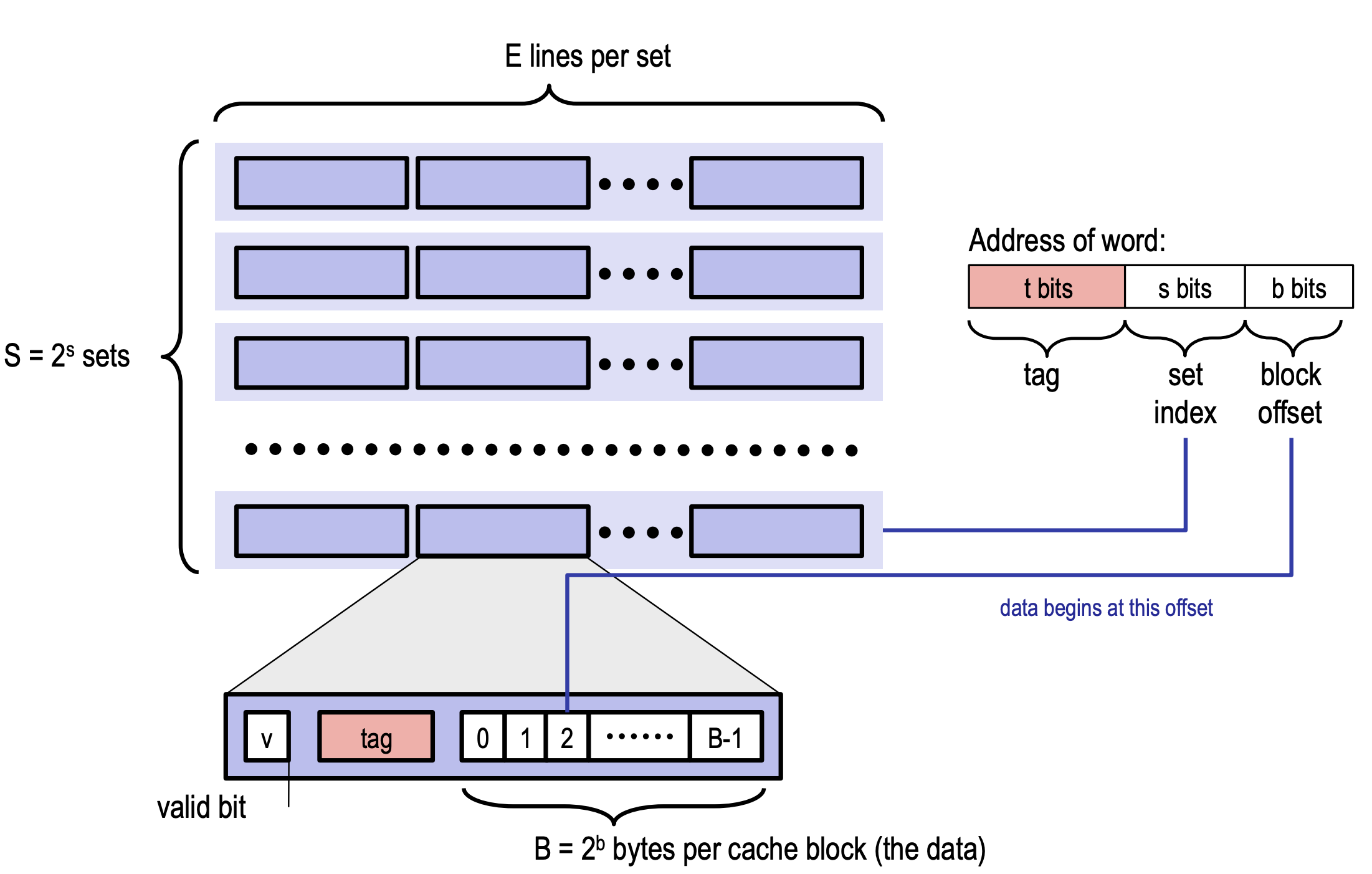
Cache 是由 $2^s$ 个 cache set 组成的集合，而每个cache set由E个cache lines组成，每个cache line 存储一个数据块block，每个数据块拥有$2^b$ 个字节，所以cache存储能力为 $S \times B \times E$，大致如下图：
Miss

当需要Block B时，如果Block B不在cache中，就需要从memory中获取Block B，这就是一次Miss。Miss可以分为三种：
- Cold miss ：第一次获取该block会得到一次miss
- Conflict miss：当cache容量足够时，当两个block发生冲突时，就会导致该block miss
- Capacity miss：当所需cache block比cache的容量大时发生，这就需要设计一种cache替换算法

Cache 替换算法

FIFO：每次替换最先进入的数据，而不考虑之前被访问的频率
LRU：每次替换最久未被访问的数据，实际应用较广
LFU：每次替换访问次数最小的数据
…

Part A: Writing a Cache Simulator

实验指导手册：lab

Cache Lab writeup：cachelab.dvi (cmu.edu)

1. 准备工作

任务要求

在csim.c中写一个cache模拟器，讲valgrind memory trace作为输入，输出：the total munber of hits，misses，and evictions。

二进制可执行问文件csim-ref作为对照，s e b分别对应 $S \times B \times E$

1	Usage: ./csim-ref [-hv] -s <s> -E <E> -b <b> -t <tracefile>

编程规则

在csim.c中添加自己的标识符。
必须在没有警告的情况下编译。
使用malloc函数，适配任意的S、E和B输入。
忽略所有的instruction cache access。
在main()末尾调用如下函数，来获取分数：

printSummary(hit_count, miss_count, eviction_count);
对于这个实验，假设内存访问是正确对齐的，且耽搁内存访问永远不会跨越block bundaries，这样就可以忽略valgrind trace中的size大小。

数据结构

按照之前的定义，cache是一个cache line的2维数组，而每个cache line 应该包含Valid bit、Tag、LRU counter。

LRU实现

HashMap + 双向循环链表：精准实现get, put方法都在O(1)的平均时间复杂度运行，但存在空间浪费。
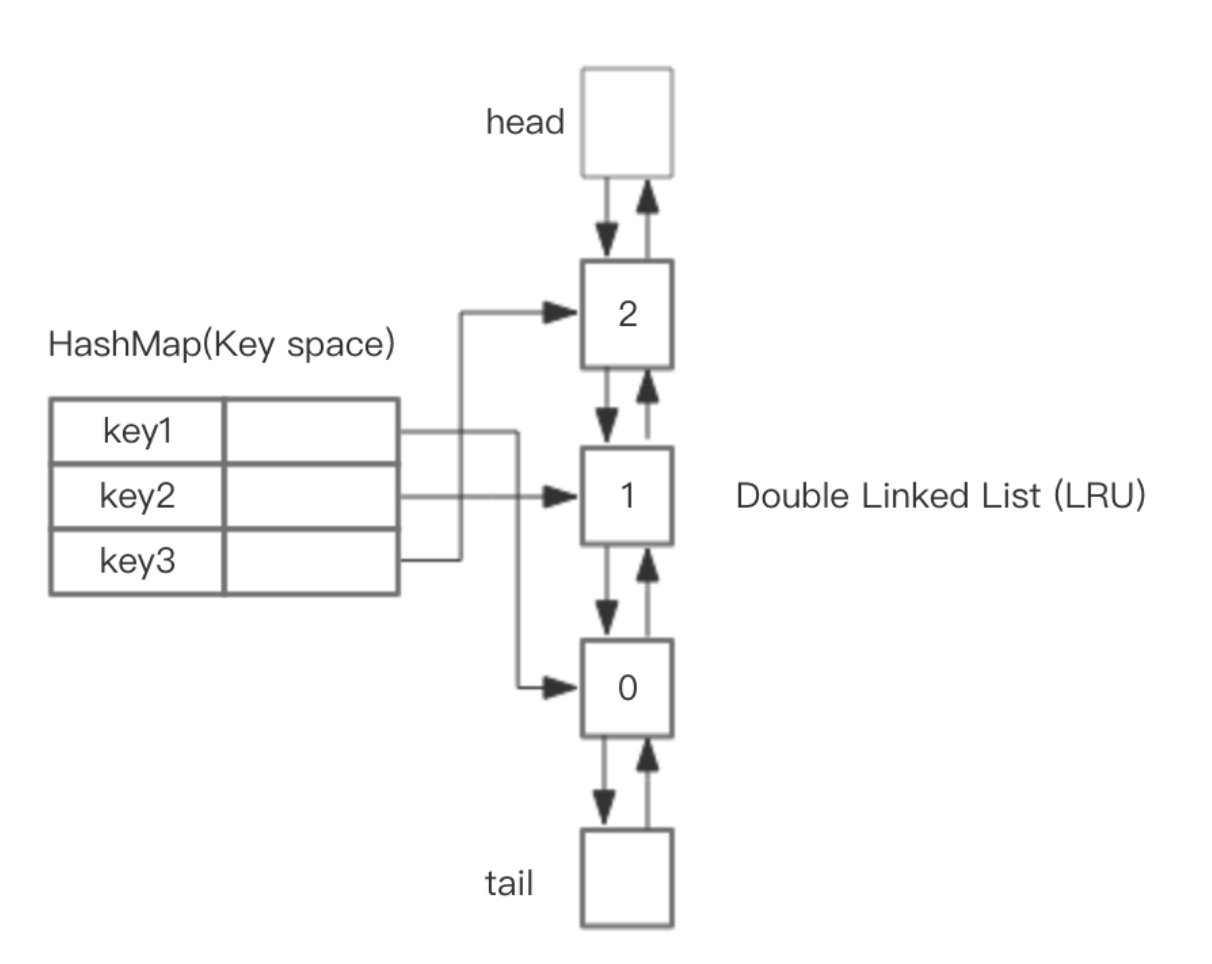
近似实现：随机取出若干个key，然后按照访问时间排序后，淘汰掉最不经常使用的。

测试用例分析

Trace Files：在traces文件夹下，由valgrind生成
每个.trace文件有n行，每一行的格式如下
1
2
3
4
5
I 0400d7d4,8
M 0421c7f0,4
L 04f6b868,8
S 7ff0005c8,8
[space] operation address,size
operation表示内存访问类型，”I” 表示指令加载，“L”表示数据加载，“S”表示数据存储，“M”表示数据修改。

address表示64-bit十六进制内存地址。

size表示操作访问的字节数。

所需函数调用

// 自动解析Unix命令行上的元素, 
// man 3 getopt (for more information)
#include <unistd.h>
getopt()
  
// 从trace files中读取数据
fscanf()
  
malloc/free

2. 实现过程与心得

1 2	make ./test-csim

首先按照利用getopt()以及fscanf()函数来处理程序输入以及trace文件读取。
首先定义cache line数据类型，以及其指针，然后malloc生成指定大小的cache。
cache逻辑：给定一个address
1. 分离出set_index与tag
2. 遍历该set的所有cache line，如果tag匹配则hit
3. 若无匹配，查看是否有空闲cache line
4. 若无空闲cache line，就进行替换，替换方法采用近似方法，可参考Redis中的LRU算法,一篇文章彻底搞懂 - 知乎 (zhihu.com)

整个实现非常简单，但是需要细心，注意文件的关闭以及cache free。最后通过的结果应该如下图：

Part B: Optimizing Matrix Transpose

1. 准备工作

任务要求

在trans.c中实现*transpose_submit()*函数，使其cache misses最小。

编程规则

最多定义总和12个int局部变量，包括子函数
不能使用递归
不能修改array A
不能malloc任何array
Cache 条件

1KB cache，E=1，b=5，s=5

所以有32个cache set，每个cache set 有一个block，每个block中可存储32个字节，也就是8个int

2. 实现过程与心得

# 32 * 32 miss < 300
# 64 * 64 miss < 1300
# 61 * 67 miss < 2000
./test-trans -M 32 -N 32

$32 \times 32$ 矩阵下

根据所给的cache，一个很自然的想法就是分块，首先考虑的是对$8 \times 8$的block进行transpose，但是测试得到只降到了343次，并不符合要求。在思考这些miss出现的原因时，可以想到，当A，B中的元素都对应同一个cache block时就会出现，这样完成八个int的赋值会多造成两次miss，所以最简单的办法就是每次赋值的时候，一次性将A的整个block中的8个int读取到局部变量中，然后再赋值给B，这样在测试时就可以得到287次miss💯
$64 \times 64$ 矩阵下

继续尝试使用$8 \times 8$的方式，得到了4611次misses，因为s=5，只有32个cache set，对于$64 \times 64$ 矩阵来说，每4行一个循环，因此会存在大量的cache冲突，第一个尝试办法就是将$8 \times 8$变为$4 \times 4$，因为每超过四行就会出现cache冲突。简单的修改后得到了1699次misses，还不能达到要求。接下来一个很自然的想法自然是重新按照$8 \times 8$进行，但是对内部进行特别优化，首先想到的就是把其分成4个$4 \times 4$，分三步走：
1. 取前4行的A，拆成两部分，一部分transpose，一部分存储至B2.1
2. 取后四行A的前半部分，并同时将B2.1复位
3. 处理B2.2
  
  最终计算示意图如下：
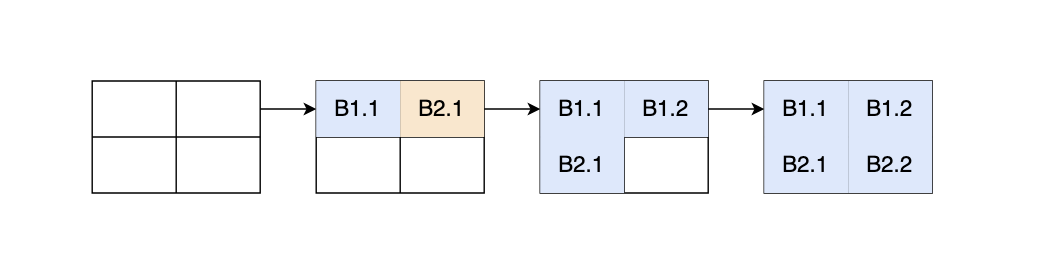
测试结果为1227次misses💯
$61 \times 67$ 矩阵下

对于不规则的矩形，我首先考虑先按照$8$个为一组进行处理，然后对于剩下的部分按照一般方法处理，最终测试得到1875次misses💯

实验过程中，不断思考目前这些cache由什么情况造成的，是由于A，B造成的冲突，还是B，B造成的冲突。